A Fast Estimator for Binary Choice Models with Spatial, Temporal, and Spatio-Temporal Interdependence
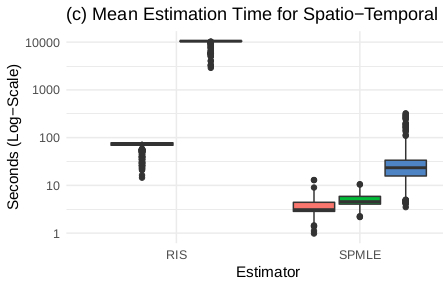 Estimation Times for RIS-Probit and Spatio-Temporal Pseudo Maximum Likelihood Estimators.
Estimation Times for RIS-Probit and Spatio-Temporal Pseudo Maximum Likelihood Estimators.
Abstract
Binary outcome models are frequently used in the social sciences and economics. However, such models are difficult to estimate with interdependent data structures, including spatial, temporal, and spatio-temporal autocorrelation because jointly determined error terms in the reduced-form specification are generally analytically intractable. To deal with this problem, simulation-based approaches have been proposed. However, these approaches (i) are computationally intensive and impractical for sizable datasets commonly used in contemporary research, and (ii) rarely address temporal interdependence. As a way forward, we demonstrate how to reduce the computational burden significantly by (i) introducing analytically-tractable pseudo maximum likelihood estimators (PMLE) for latent binary choice models that exhibit interdependence across space \emph{and} time and by (ii) proposing an implementation strategy that increases computational efficiency considerably. Monte Carlo experiments show that our estimators recover the parameter values as good as commonly-used estimation alternatives and require only a fraction of the computational cost.